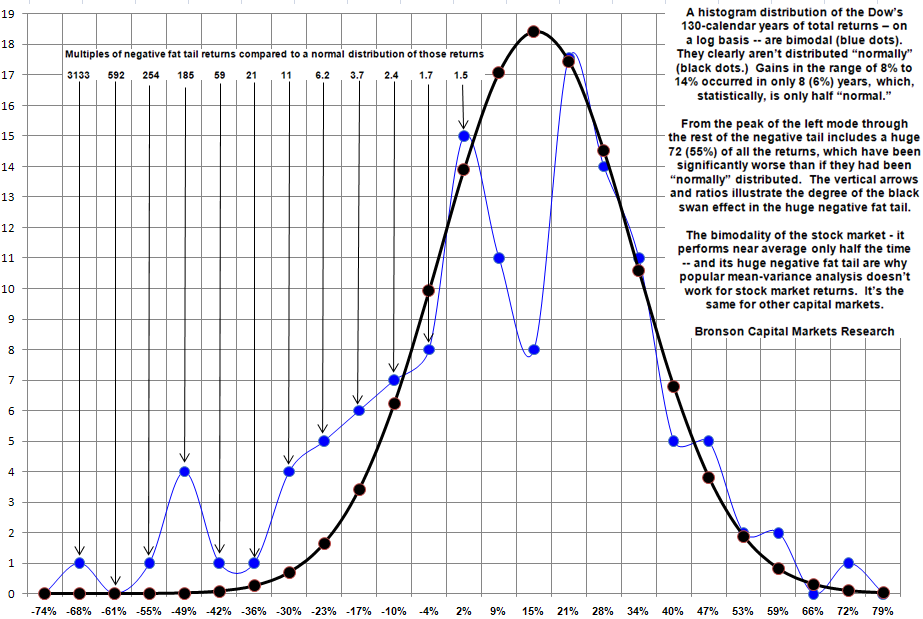
Via Bob Bronson, we get this very interesting way to think about the potential universe of market returns:
In addition to the almost universally improper use of the correlation function that we have presented before (our Correlation Puzzle is available on request), Alpha-Beta, Efficient Frontier, Black Scholes, VaR, stochastic modeling, and exotic derivatives from Modern Portfolio Theory and Post-Modern Portfolio Theory also variously depend on security returns being “normally” distributed, but it is demonstrable that they are not for any capital market over any time scale.
Don’t confuse the distribution of returns on a log-scale versus an arithmetic scale – see those chart comparisons further below. A common mistake made by many, especially on internet blogs, is not understanding the huge application difference between application of logarithms and percentages. A good example is the systemic drift with index funds and ETFs, especially the high (beta) multiple inverse ones.


What's been said:
Discussions found on the web: